【RNN基礎】RNNとはなにか？Pythonで実装しながらちゃんと理解してみる。

当ページのリンクには広告が含まれています。

✓目次

• 本記事の対象者
• RNNとはなにか
• RNNは勾配爆発と勾配消失を起こしやすい
• RNNを実装してみる
  • 訓練用データを作成する。
    • ①ノイズ付きサイン関数の作成
    • ②入力データと正解データの作成
    • ③入力データと正解データの形状をKerasのRNN仕様に変更する。
  • RNNの構築
    • バッチサイズとモデルの設定
    • モデルを作成し層を追加
  • 構築したRNNのモデルを用いて学習
  • 学習の推移を確認する。
  • 学習済モデルを使ってサイン関数を予測
• まとめ

本記事の対象者

• ニューラルネットワークとは何かを理解している人。
  
  
• pythonの基本を理解している人。
  
  
• Kerasでニューラルネットワークを作ったことがある人
  
  

以下の記事で、Kerasを使ってニューラルネットワークとはどのようなものかをまとめているので、参考にしてみてください。

>> ニューラルネットワークとは何かを学ぶ

RNNとはなにか

RNNは「リカレントニューラルネットワーク」の略です。

RNNとは、過去のデータを基に、これからどのような処理をするのかを判断することが得意なニューラルネットワークです。

時系列データを扱うのが得意なニューラルネットワークとも言われ、具体的には以下のような時系列データをあつかったりします。

• 株価
  
  
• 音声データ
  
  
• 音楽
  
  
• 文書
  
  
• 気象
  
  

RNNではこの時系列データを入力および正解として扱います。

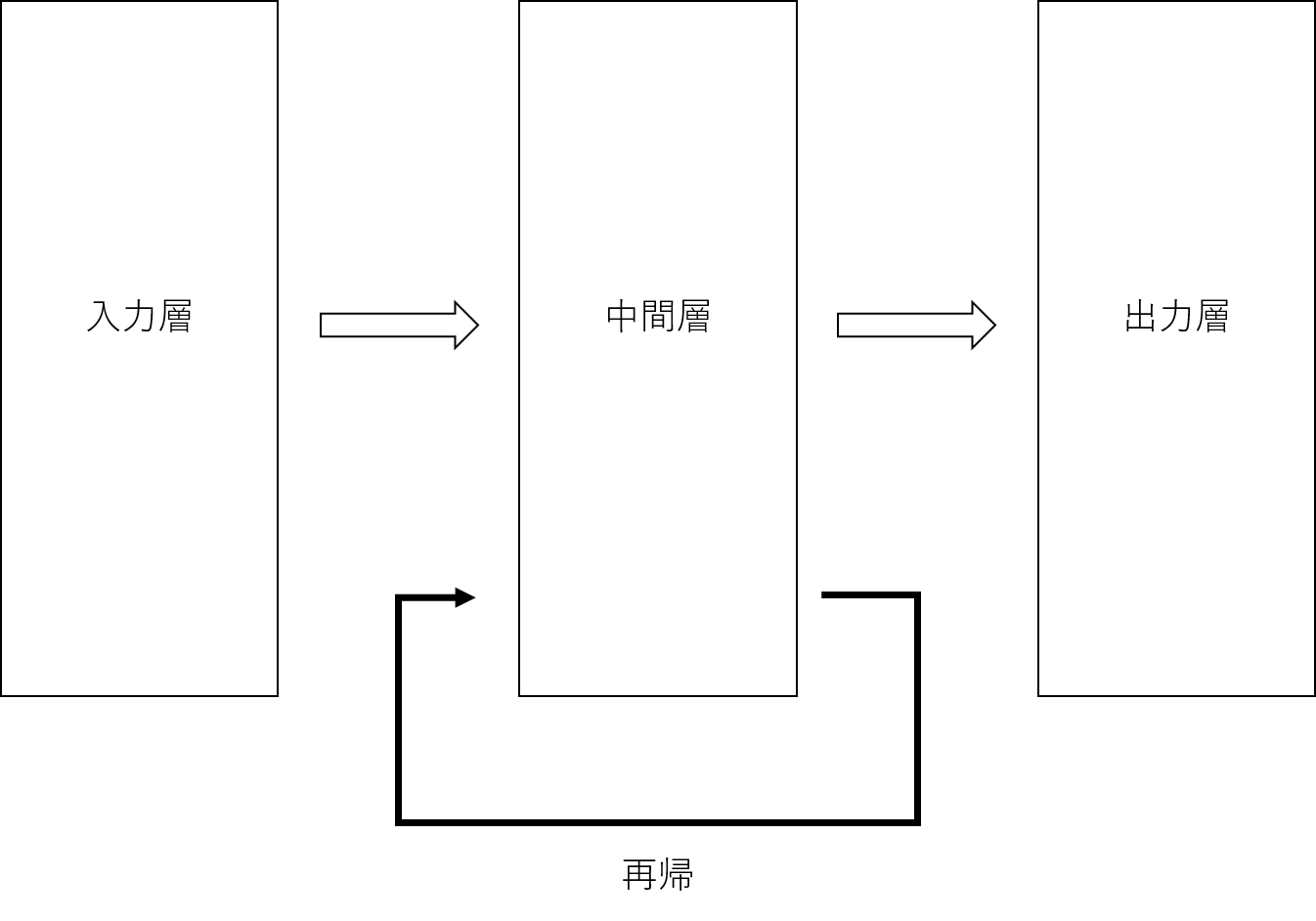
RNNの特徴は、以下の図に示すように、中間層がループする構造を取る点です。

中間層がループする構造とは、中間層の出力が入力層からの次の入力とセットで、中間層への入力になるということです。

このように、自ら出力したデータを再び入力データとしてループすることを再帰といいます。

そのためRNNは、「再帰型ニューラルネットワーク」と言い換えられたりもします。

このような特徴から、RNNは過去のデータを保持することになるため、過去のデータを用いて判断を行うことができるのです。

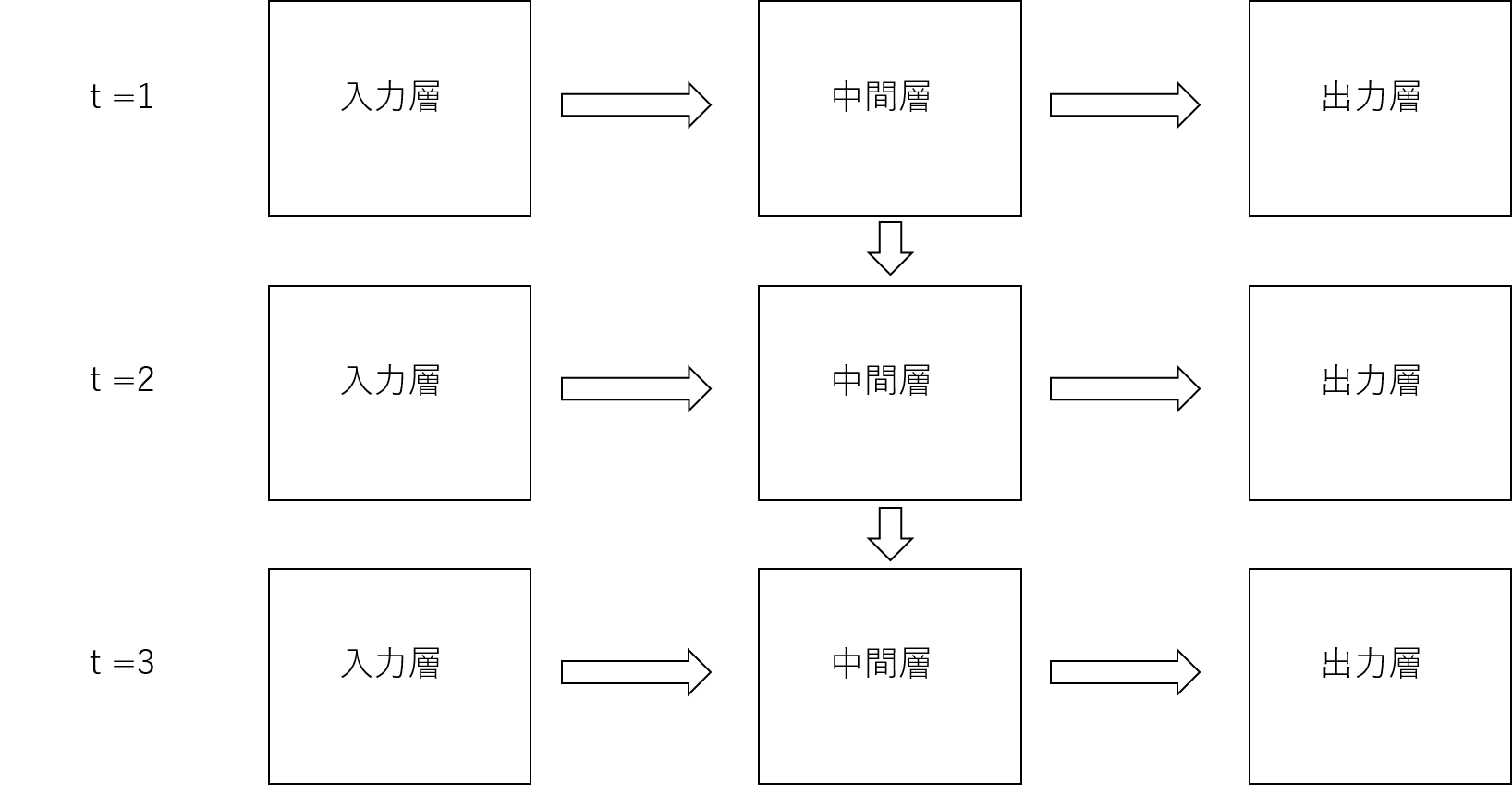
時間\( t\)の経過に沿った動作を図で表すと以下のようになります。

時間が経過すればするほど、中間層が何層にもつながり、ある意味深いニューラルネットワークになることが分かります。

順伝播で入力データに対する予測が行われ、逆伝播の際に学習が行われます。

重みの更新は、通常のニューラルネットワークと同様、以下の式で表される勾配に基づいて行われます。

RNNと通常のニューラルネットワークとの違いは、重みやバイアスのパラメータ更新に、過去のデータからさかのぼってきた情報を利用する点にあります。

つまり、全時刻を通じて誤差をさかのぼり、重みとバイアスを更新するということになります。

RNNは勾配爆発と勾配消失を起こしやすい

RNNは時系列データを用いて深いニューラルネットワークになっています。

このような構造を取った場合、何層にもわたって誤差を伝搬させることにより、勾配が大きくなりすぎるという問題が発生します。

勾配が大きくなりすぎてしまうことを勾配爆発と一般的に言い、これが起きてしまうとコンピュータ側で処理できなくなってします。

また、その逆で勾配が小さくなりすぎてしまう、勾配消失（勾配が0になる）というのも起こることがあり、学習できなくなってしまいます。

RNNは、前の時刻からデータを引継ぎ、繰り返し同じ重みを掛け合わせるため、通常のニューラルネットワークと比べて、これらの問題が起こりやすいと考えられています。

勾配爆発の対策としては、勾配クリッピングが有効です。勾配クリッピングとは、勾配の大きさに制限をかけることにより、勾配爆発を抑制することです。

勾配消失の対策としては、活性化関数を変更するか、LSTMというRNNの発展形であるニューラルネットワークを用いるのが良いそうです。

RNNを実装してみる

Jupyter NotebookでRNNの実装を行います。

Jupyter Notebookの環境構築方法は、こちらにまとめています。

ここでは、ノイズを含めたサイン関数を用意し、RNNを構築し、学習させたあと、学習済みモデルを使用して予測を行ってみたいと思います。

訓練用データを作成する。

まずは、RNNで用いる訓練用のデータを作成します。

①ノイズ付きサイン関数の作成

サイン関数に代入する値として、\( -2π\)から\( 2π\)までの値を用意します。

1
2
3
4
5
6

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

x_data = np.linspace(-2*np.pi, 2*np.pi)  # -2πから2πまで値を50個

x_dataは以下のようになっています。

1
2
3
4
5
6
7
8
9
10

array([-6.28318531, -6.02672876, -5.77027222, -5.51381568, -5.25735913,
       -5.00090259, -4.74444605, -4.48798951, -4.23153296, -3.97507642,
       -3.71861988, -3.46216333, -3.20570679, -2.94925025, -2.6927937 ,
       -2.43633716, -2.17988062, -1.92342407, -1.66696753, -1.41051099,
       -1.15405444, -0.8975979 , -0.64114136, -0.38468481, -0.12822827,
        0.12822827,  0.38468481,  0.64114136,  0.8975979 ,  1.15405444,
        1.41051099,  1.66696753,  1.92342407,  2.17988062,  2.43633716,
        2.6927937 ,  2.94925025,  3.20570679,  3.46216333,  3.71861988,
        3.97507642,  4.23153296,  4.48798951,  4.74444605,  5.00090259,
        5.25735913,  5.51381568,  5.77027222,  6.02672876,  6.28318531])

このx_dataをサイン関数に代入し、np.random.randnにより、乱数でノイズを加えてsin_dataとします。

グラフとして描画も実施します。

1
2
3
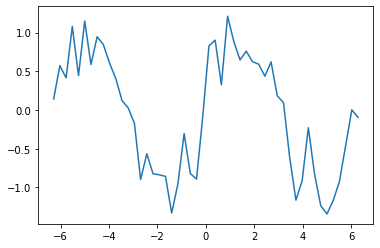
4

sin_data = np.sin(x_data)  + 0.3*np.random.randn(len(x_data))  # sin関数に乱数でノイズを加える

plt.plot(x_data, sin_data)
plt.show()

サイン関数にノイズが付いたプロットが表示されました。

②入力データと正解データの作成

続いて入力データと正解データを作りたいと思います。

1
2
3
4

n_rnn = 15  # 時系列の数
n_sample = len(x_data)-n_rnn  # サンプル数
i_data = np.zeros((n_sample, n_rnn))  # 入力
c_data = np.zeros((n_sample, n_rnn))  # 正解

まず、時系列の数を設定します。

時系列の数というのは、要するに中間層がループする回数です。

今回は15回中間層がループする設定にします。

サンプル数は、len(x_data)-n_rnnとなり、今回の例でいうと、50 - 15 = 35となります。

これは、入力データと正解データを1セットで1サンプルとしてカウントするためです。

具体的に説明します。

x_data（データ数：50）に対して、時系列の数である15個分のデータを1つのブロックとし、これを入力データとします。

そして、入力データから値を予想するモデルを作るために必要な正解データとして、入力データを1つずらした15個分のデータ1ブロックを正解データとします。

そして1サンプルというのは、先に述べた入力データおよび正解データの2つを1セットにしたものを指します。

図で表すと以下のようなイメージです。

入力データであるi_dataは、numpyのzerosメソッドで、すべて0とし初期化しておきます。

i_dataの行数は、サンプル数であるn_sampleとし、列数は時系列の数であるn_rnnにします。

正解データに関しても同様の配列にします。

i_data.shapeを実行すると(35, 15)、つまり、35行、15列になっていることが分かります。

もちろん配列データの中身は[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]となっています。

次に初期化したi_dataとc_dataに、sin関数にノイズを加えたsin_dataを設定していきます。

1
2
3

for i in range(0, n_sample):
    i_data[i] = sin_data[i:i+n_rnn]
    c_data[i] = sin_data[i+1:i+n_rnn+1]  # 時系列を入力よりも一つ後にずらす

入力データi_dataは、iからi+n_rnnまでを1ブロックとして加えたものになります。

正解データc_dataは時系列を入力データよりも1つ後にずらしたものになります。

未来のデータであればsin_data[i+n_rnn+1]の一つだけでも良さそうですが、これではエラーになります。

RNNには2つのタイプがあり、最後の時刻のみの出力を使うタイプと、全ての時刻の出力を使うタイプです。

前者に必要な正解は1つですが、後者は出力の数だけ正解が必要になります。

今回は後者にあたります。

上記のコードを実行し、i_dataの中身を見てみると、以下のようになっています。

1
2
3
4
5
6
7
8

array([[-0.03454036,  0.24525829,  0.58367546,  0.78578144,  1.29077749,
         0.68850031,  0.81436868,  0.60852433,  1.17917601,  0.83042115,
         0.73981007,  0.71591622,  0.20791259, -0.13519872, -0.41113603],
       [ 0.24525829,  0.58367546,  0.78578144,  1.29077749,  0.68850031,
         0.81436868,  0.60852433,  1.17917601,  0.83042115,  0.73981007,
         0.71591622,  0.20791259, -0.13519872, -0.41113603, -0.52893013],

        (略)

③入力データと正解データの形状をKerasのRNN仕様に変更する。

入力と正解データを作成しましたが、Kerasでは、データの形状を(入力のサンプル数, 時系列の数, 入力層のニューロン数)にする必要があります。

現時点でのi_dataの形状は、(35, 15)になっているので、reshapeを用いて、形状を変更させます。

1
2

i_data = i_data.reshape(n_sample, n_rnn, 1)  # KerasにおけるRNNでは、入力を（サンプル数、時系列の数、入力層のニューロン数）にする
c_data = c_data.reshape(n_sample, n_rnn, 1)  # 今回は入力と同じ形状

i_dataの中身を見てみると以下のようになっており、形状は(35, 15, 1)となります。

それぞれサンプル数、時系列の数、入力層のニューロン数を表しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

array([[[-0.03454036],
        [ 0.24525829],
        [ 0.58367546],
        [ 0.78578144],
        [ 1.29077749],
        [ 0.68850031],
        [ 0.81436868],
        [ 0.60852433],
        [ 1.17917601],
        [ 0.83042115],
        [ 0.73981007],
        [ 0.71591622],
        [ 0.20791259],
        [-0.13519872],
        [-0.41113603]],

       [[ 0.24525829],
        [ 0.58367546],
        [ 0.78578144],
        [ 1.29077749],
        [ 0.68850031],
        [ 0.81436868],
        [ 0.60852433],
        [ 1.17917601],
        [ 0.83042115],
        [ 0.73981007],
        [ 0.71591622],
        [ 0.20791259],
        [-0.13519872],
        [-0.41113603],
        [-0.52893013]],


        (略)

これで、訓練用のデータを作成することができました。

RNNの構築

Kerasを使ってRNNを構築します。

Kerasで活用できるRNNは主に以下があります。

• SimpleRNN: RNN。全結合の中間層が再帰的になる。
• LSTM: RNNの発展版であるLSTMを活用できる。複雑な時系列データを扱えるが学習に時間がかかる。
• GRU: LSTMの簡易版のようなもの。LSTMに比べパラメータが少ないので、LSTMに比べて学習に時間がかからない。

お好みに合わせて、何れかのニューラルネットワークを活用すればよいと思います。

バッチサイズとモデルの設定

本記事では、Kerasで活用できるRNNの中で一番シンプルな、SimpleRNN層を使います。

バッチサイズ、入力層のニューロン数、中間層のニューロン数、出力層のニューロン数を設定します。

1
2
3
4
5
6
7

from keras.models import Sequential
from keras.layers import Dense, SimpleRNN

batch_size = 5  # バッチサイズ
n_in = 1  # 入力層のニューロン数
n_mid = 20  # 中間層のニューロン数
n_out = 1  # 出力層のニューロン数

これでOKです。

モデルを作成し層を追加

Sequential()でモデルを作成し、層を追加していきます。

1
2
3
4
5
6
7

model = Sequential()
# SimpleRNN層の追加。return_sequenceをTrueにすると、時系列の全てのRNN層が出力を返す。
# return_sequenceをTrueをFalseにすると、最後のRNN層のみが出力を返す。
model.add(SimpleRNN(n_mid, input_shape=(n_rnn, n_in), return_sequences=True))
model.add(Dense(n_out, activation="linear"))
model.compile(loss="mean_squared_error", optimizer="sgd")  # 誤差は二乗誤差、最適化アルゴリズムはSGD
print(model.summary())

まずはSimpleRNNの層を追加します。

SimpleRNN追加の際は、中間層のニューロン数を設定して、入力の形状を設定します。

RNNの場合、入力の形状は、(時系列の数(15), 入力層のニューロン数(1))となります。

return_sequencesはTrueに設定します。Trueにすることで、時系列のすべてのRNN層が出力を返すことになります。これをFalseに設定すると、最後のRNN層のみが、出力を返すことになります。なお、デフォルトでは、この値はFalseになっています。

SimpleRNNの後は、Denceを追加します。

Denceは通常のニューラルネットワークにおける、全結合層になります。

Denceには、出力層のニューロン数を設定し、活性化関数を、linearに設定します。linearは、恒等関数です。

SimpleRNNでは、活性化関数を設定していませんが、SimpleRNNの標準としてtanh(ハイパボリックタンジェント)が設定されます。

最後に、compileを行います。

損失関数は、回帰の場合は二乗誤差を適用し、分類の場合はクロスエントロピーを適用するのが一般的です。今回は、回帰になるので二乗誤差を設定します。

最適化アルゴリズムには、SDGを使用します。

こちらのコードを実行すると、model.summary()によって、以下のような出力を得ることが来ます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn_2 (SimpleRNN)     (None, 15, 20)            440       
_________________________________________________________________
dense_2 (Dense)              (None, 15, 1)             21        
=================================================================
Total params: 461
Trainable params: 461
Non-trainable params: 0
_________________________________________________________________
None

SimpleRNNのOutput Shapeは(None, 15, 20)となっています。15は時系列の数、20は中間層のニューロン数を意味しています。

パラメータの数は、合計で461であることが分かります。

SimpleRNNのパラメータ数は440であることが分かります。440の内訳は以下の通りです。

• 入力に対しての重み
  入力の次元数ｘ隠れ状態の次元数　
  →　1*20

• 隠れ状態に対しての重み
  隠れ状態の次元数 x 隠れ状態の次元数
  →　20*20

• バイアス
  隠れ状態の次元数
  →　20

その他のパタンのパラメータ数の数え方については、こちらの記事で分かりやすくまとめられてます。

DenseのOutput Shapeは(None, 15, 1)となっています。15は時系列の数、1は出力層のニューロン数を意味しています。

参考ですが、重みやバイアスを調べる方法を以下にまとめます。

1
2
3
4
5
6
7
8
9

print(len(model.layers[0].get_weights()))
# 3
i_weight, h_weight, bias = model.layers[0].get_weights() # lenが3なので、3変数に代入
print(i_weight.size)
# 20
print(h_weight.size)
# 400
print(bias.size)
# 20

構築したRNNのモデルを用いて学習

学習は、fitメソッドを用いて行う。

入力データ(i_data)、正解データ(c_data)のほかにエポック数を指定する。

またバッチサイズとバリデーションスプリットも指定を行う。

1

history = model.fit(i_data, c_data, epochs=100, batch_size=batch_size, validation_split=0.1)

すると以下のように学習が走ります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Train on 31 samples, validate on 4 samples
Epoch 1/100
31/31 [==============================] - 0s 5ms/step - loss: 0.3232 - val_loss: 0.2373
Epoch 2/100
31/31 [==============================] - 0s 631us/step - loss: 0.2265 - val_loss: 0.2034
Epoch 3/100
31/31 [==============================] - 0s 551us/step - loss: 0.2003 - val_loss: 0.1930

(略)

Epoch 98/100
31/31 [==============================] - 0s 500us/step - loss: 0.1233 - val_loss: 0.1471
Epoch 99/100
31/31 [==============================] - 0s 505us/step - loss: 0.1233 - val_loss: 0.1467
Epoch 100/100
31/31 [==============================] - 0s 490us/step - loss: 0.1230 - val_loss: 0.1468

学習の推移を確認する。

lossとval_lossを確認していきましょう。

1
2
3
4
5
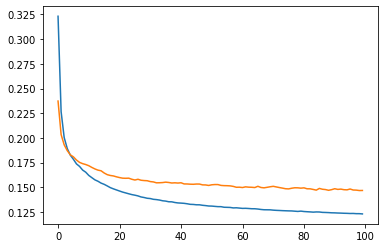
6

loss = history.history['loss']
vloss = history.history['val_loss']

plt.plot(np.arange(len(loss)), loss)
plt.plot(np.arange(len(vloss)), vloss)
plt.show()

訓練用のデータ、検証用のデータ、共に収束していることが分かります。

学習済モデルを使ってサイン関数を予測

入力データを用います。

入力データ(i_data)とは何なのかをおさらいすると、、x_data（データ数：50）に対して、時系列の数である15個分のデータを1つのブロックとし、このブロックが合計で35個あるデータでした。

i_data.shapeを実行すると(35, 15, 1)と出力されることからも理解ができると思います。

入力データから最初の行列取り出し、reshape(-1)で1次元のベクトルにし、predictedという変数に格納します。

1
2

predicted = i_data[0].reshape(-1)  # 入力データの最初の行列データを取り出し、reshape(-1)で一次元のベクトルにする。
predicted

これを実行すると、以下のように出力されます。

1
2
3

array([-0.29245656,  0.33761251,  0.73473534,  0.88417973,  0.8520399 ,
        0.91658402,  1.33572366,  0.84339794,  1.00440569,  0.45843943,
        0.56022552,  0.23427566,  0.10704196, -0.65186734, -0.73755624])

次に、この入力データ(predicted)を学習済みのモデルに入力し、値の予測をさせてみたいと思います。

以下のfor文になります。

1
2
3

for i in range(0, n_sample):
    y = model.predict(predicted[-n_rnn:].reshape(1, n_rnn, 1))  # 直近のデータを使って予測を行う
    predicted = np.append(predicted, y[0][n_rnn-1][0])  # 出力の最後の結果をpredictedに追加する

最初のforループでは、predicted[0:]となるので、predictedに代入されているすべての15データを使って予測をしています。

その後、予測値yの末尾をpredictedに追加しています。

2回目以降のループでは、前回の予測値yの末尾を含んだ直近のデータ15個で予測をしています。

そのため、2回目のループでは、「predictの先頭のデータを除いた14個のデータ」 ＋ 「末尾に加えられた予測値yのデータ」の合計、15個のデータで予測を行っています。

そのため、ループの16回目からは、もともとのpredictのデータは全く使われず、すべて予測値yのデータで、追加予測をしていることになります。

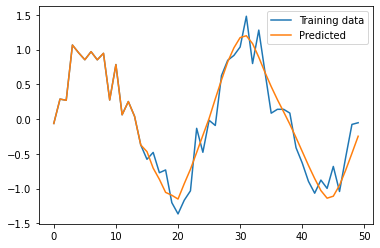
予測結果を確認してみます。比較のために、sin_dataも同時にプロットします。

1
2
3
4

plt.plot(np.arange(len(sin_data)), sin_data, label="Training data")
plt.plot(np.arange(len(predicted)), predicted, label="Predicted")
plt.legend()
plt.show()

青いラインが訓練用のデータで、オレンジのラインが学習済みのRNNのモデルで予測した結果です。

このように、直近の時系列データを使って、次の値を予測できるようになりました。

直近のデータを加えながら予測を行っているため、グラフが右に進めば進むほど、誤差の影響が積み重なるように受けてしまうため、訓練用データとのずれが大きくなっていることが確認できます。

まとめ

今回は、sin関数の予測を行いました。

cos関数の予測に挑戦してみたり、各設定値を変えたり、実際の時系列データ（株価等）に適用してみたりすれば、より理解を深められると思います。

本記事が役立ったらTwitterのフォローもよろしくおねがいします！

RNNについてさらなる応用を学びたい方は、以下のUdemyを参照してください。

【キカガク流】人工知能・機械学習 脱ブラックボックス講座 - 初級編 -

自然言語処理とチャットボット: AIによる文章生成と会話エンジン開発

参考記事

• https://note.nkmk.me/python-tensorflow-keras-count-params/

• https://note.nkmk.me/python-tensorflow-keras-get-weights-kernel-bias/

• https://qiita.com/Phoeboooo/items/6c3ea770047c820046f4