【Keras】ニューラルネットワーク(NN)をPythonで作成する方法

当ページのリンクには広告が含まれています。

ニューラルネットワークとはどのようなものかをkerasという機械学習を簡単に使うためのライブラリを使ってまとめました。高校の数学でならったsin(サイン)関数をつかって、学習→予測をしてみたいと思います。

目次

• 本記事の対象者: ニューラルネットワーク(NN)をPythonで実装する方法を知りたい人
• Pythonの環境
• Kerasで作成するニューラルネットワーク(NN)の学習データの準備
  • 入力データxの作成
  • 正解データ（sin関数）の作成とグラフ描画
• Kerasでニューラルネットワーク(NN)の構築、学習、予測
  • ニューラルネットワークの設定
  • ニューラルネットワークの構築
    • 1セット目(入力層と中間層)の追加
    • 2セット目(中間層と出力層)の追加
    • コンパイル
  • ニューラルネットワークを用いて学習
    • 学習の推移をグラフで確認
  • 学習済ニューラルネットワークを使用して予測
• Kerasでニューラルネットワーク(NN)を構築し学習/訓練、予測させる方法をまとめました。

本記事の対象者: ニューラルネットワーク(NN)をPythonで実装する方法を知りたい人

• ニューラルネットワーク、というものがなんとなくわかっているが、細かい言葉の定義とかを忘れてしまった人。（順伝播、逆伝播とかを知っている。）
• 高校の数学（特に三角関数）を理解している。
• pythonのプログラミングを、それなりに理解している。（progate等でpythonの使い方を雰囲気程度で理解している）
• これから本格的に、ニューラルネットワークを学ぶために基本的なことを復習したい人。

Pythonの環境

以下の記事で紹介しているように、Anaconda NavigatorでJupyter notebookの環境を整えてください。

もしくは、Google Colaboratoryという、Google chromeというブラウザのみでプログラミングができる環境を使ってもいいと思います。

https://colab.research.google.com/?hl=ja

Kerasで作成するニューラルネットワーク(NN)の学習データの準備

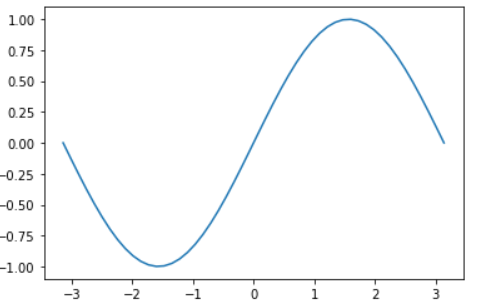
本記事では、データの例としてサイン関数を用意したいと思います。

入力データをx, 正解データをtとします。

入力データxの作成

まずは入力データとなるxを作成します。

ソースコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi).reshape(-1, 1)

print(x)

numpyとmatplotlibというライブラリをインポート。

入力xとしてnp.linspace(-np.pi, np.pi).reshape(-1, 1)と記載していますが、これは、-πからπまでの値を50行、1列の行列データを作成しています。

linspace()というのは、値の範囲を指定するメソッドです。ここで、-np.pi, np.piとすることで、-π(-3.1415・・・)からπ(3.1415・・・)までの範囲の値を扱うことを宣言しています。

reshape()は、行数と列数を指定して、行列の形を指定したり変更したりするメソッドです。

このコードでは、reshape(-1, 1)、すなわち行数を-1, 列数を1としています。行数が-1ってどのような意味なのかというと、-1を指定することで、「良い具合に自動で列数決めてくださいね。」というメッセージを送っていることになります。

良い具合に、というのは、reshapeの大本であるlinspaceにおけるデフォルト設定のことを指しており、具体的な数値でいうと50が設定されます。

すなわち、-πからπまでの値を50等分した配列データを作成しています。

作成したxをプリントすると以下のようになります。

[[-3.14159265]
 [-3.01336438]
 [-2.88513611]
 [-2.75690784]
 [-2.62867957]
 [-2.5004513 ]
 [-2.37222302]
 [-2.24399475]
 [-2.11576648]
 [-1.98753821]
 [-1.85930994]
 [-1.73108167]
 [-1.60285339]
 [-1.47462512]
 [-1.34639685]
 [-1.21816858]
 [-1.08994031]
 [-0.96171204]
 [-0.83348377]
 [-0.70525549]
 [-0.57702722]
 [-0.44879895]
 [-0.32057068]
 [-0.19234241]
 [-0.06411414]
 [ 0.06411414]
 [ 0.19234241]
 [ 0.32057068]
 [ 0.44879895]
 [ 0.57702722]
 [ 0.70525549]
 [ 0.83348377]
 [ 0.96171204]
 [ 1.08994031]
 [ 1.21816858]
 [ 1.34639685]
 [ 1.47462512]
 [ 1.60285339]
 [ 1.73108167]
 [ 1.85930994]
 [ 1.98753821]
 [ 2.11576648]
 [ 2.24399475]
 [ 2.37222302]
 [ 2.5004513 ]
 [ 2.62867957]
 [ 2.75690784]
 [ 2.88513611]
 [ 3.01336438]
 [ 3.14159265]]

これで入力データは完成です。

正解データ（sin関数）の作成とグラフ描画

続いて、正解データであるtを用意します。

ソースコードは以下です。

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi).reshape(-1, 1) 
print(x)

t = np.sin(x)  # sin関数

plt.plot(x, t)
plt.show()

1行目の、%matplotlib inlineですが、実はこれが記載されていないとJupyter Notebook環境でグラフが表示されません。おまじないのように記載しておきましょう。

3行目から7行目は、先ほどの入力データxで説明した箇所なので、説明は省きます。

9行目のt = np.sin(x)で、先ほどの入力データxをサイン関数にいれて、これを正解データtとしています。

そして、plt.plot(x, t)で、横軸をx、縦軸をtとし、plt.show()とすることで、描画したグラフを出力させます。※plt.show()の記述が無くてもグラフが描画されたりしますが、そこは気にしない。

コードを実行すると以下のようにサイン関数のグラフが出力されます。

Kerasでニューラルネットワーク(NN)の構築、学習、予測

ここから、Kerasを使ってニューラルネットワークの構築し、sin関数を学習し、入力データを用いて予測を行います。

ここで構築するのは、入力層のニューロン数が1, 中間層のニューロン数が20、出力層のニューロン数が1の3層のニューラルネットワークです。

ニューラルネットワークの設定

ソースコードは以下の通りです。

from keras.models import Sequential
from keras.layers import Dense

# ニューラルネットワークの設定
n_in = 1  # 入力層のニューロン数
n_mid = 20  # 中間層のニューロン数
n_out = 1  # 出力層のニューロン数

batch_size = 8  # バッチサイズ

# 入力層、中間層、出力層の３層のニューラルネットワークを構築
model = Sequential()
model.add(Dense(n_mid, input_shape=(n_in,), activation="sigmoid"))  # 活性化関数にシグモイド関数
model.add(Dense(n_out, activation="linear"))  # 活性化関数に恒等関数
model.compile(loss="mean_squared_error", optimizer="sgd")  # 損失関数に二乗誤差、最適化アルゴリズムにSGDを使用してコンパイル
print(model.summary())

少し複雑に思うかもしれませんが、一つ一つ説明していきます。

入力層のニューロン数が1, 中間層のニューロン数が20、出力層のニューロン数が1、なのでニューラルネットワークの設定として、

• 入力層のニューロン数をn_in = 1
• 中間層のニューロン数をn_mid = 20
• 出力層のニューロン数をn_out = 1

という風に記載します。

続いて、バッチサイズを8と設定しています。

バッチサイズとは、膨大なデータを細かく分割する単位の数です。

例えば、100万個のサンプルがあったとします。

これに対してバッチサイズを100と設定した場合、100万のサンプルを100個ずつ細かく分割し、1万個の小さい100個入りの箱に分けるということです。

この箱の一つ一つをミニバッチといい、ミニバッチに分けて計算することをミニバッチ学習と言います。

ミニバッチ学習をすると何が嬉しいのでしょうか。

100万個のサンプルの計算というのは基本的に多くの時間がかかり、1回の更新を終えるだけで膨大な時間を要します。

しかし、ミニバッチ学習を採用することで、誤差を修正する更新を終える頻度を増やすことができます。

そのため、どのように値が更新されたのかを観察しやすく、かつ、更新頻度を増やすことで、サンプル全体として最適な値を導くことができ、局所解を防ぐことができます。

なお、100万個のサンプル全体の計算を終えて、パラメータの更新が1回終わることを、1epoc(エポック)と言います。

そして、ミニバッチのパラメータを更新することを1 iteration(イテレーション)と言います。

今回の例でいうと、100万サンプルを100ずつ細かく分割し1万の小さい箱に分けているので、1epoch = 1万iterationとなります。

これで、「バッチサイズ」、「ミニバッチ」、「ミニバッチ学習」、「エポック」、「イテレーション」というものの概要が理解できたかと思います。

ニューラルネットワークの構築

続いて、入力層、中間層、出力層の３層のニューラルネットワークを構築していきます。

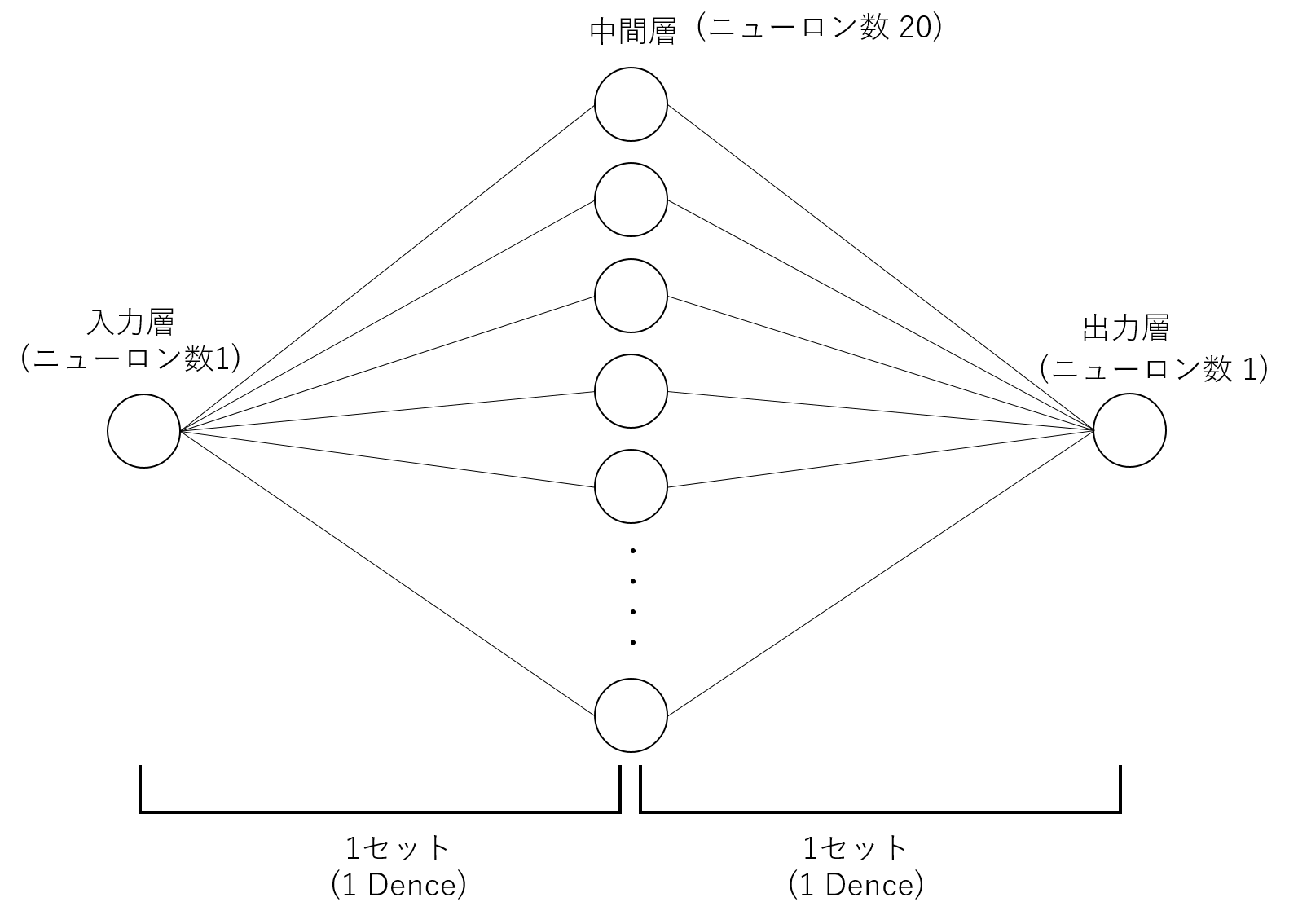
3層のニューラルネットワークを構築する前に、ニューラルネットワークを構築する際の考え方として大事なのは、2層を1セットで考えるということです。

つまり、下図に示すように「入力層と中間層」で1セット、「中間層と出力層」で1セット、合計2セットとして扱うということです。

それぞれの1セットは、Dence()を用いて追加します。

1セット目(入力層と中間層)の追加

Denseは、Sequential()を用いてmodelを作成し、addメソッドによって活用されます。

コードでいうと、1セット目(入力層と中間層)の部分はmodel.add(Dense(n_mid, input_shape=(n_in,), activation="sigmoid"))という風にして追加しています。

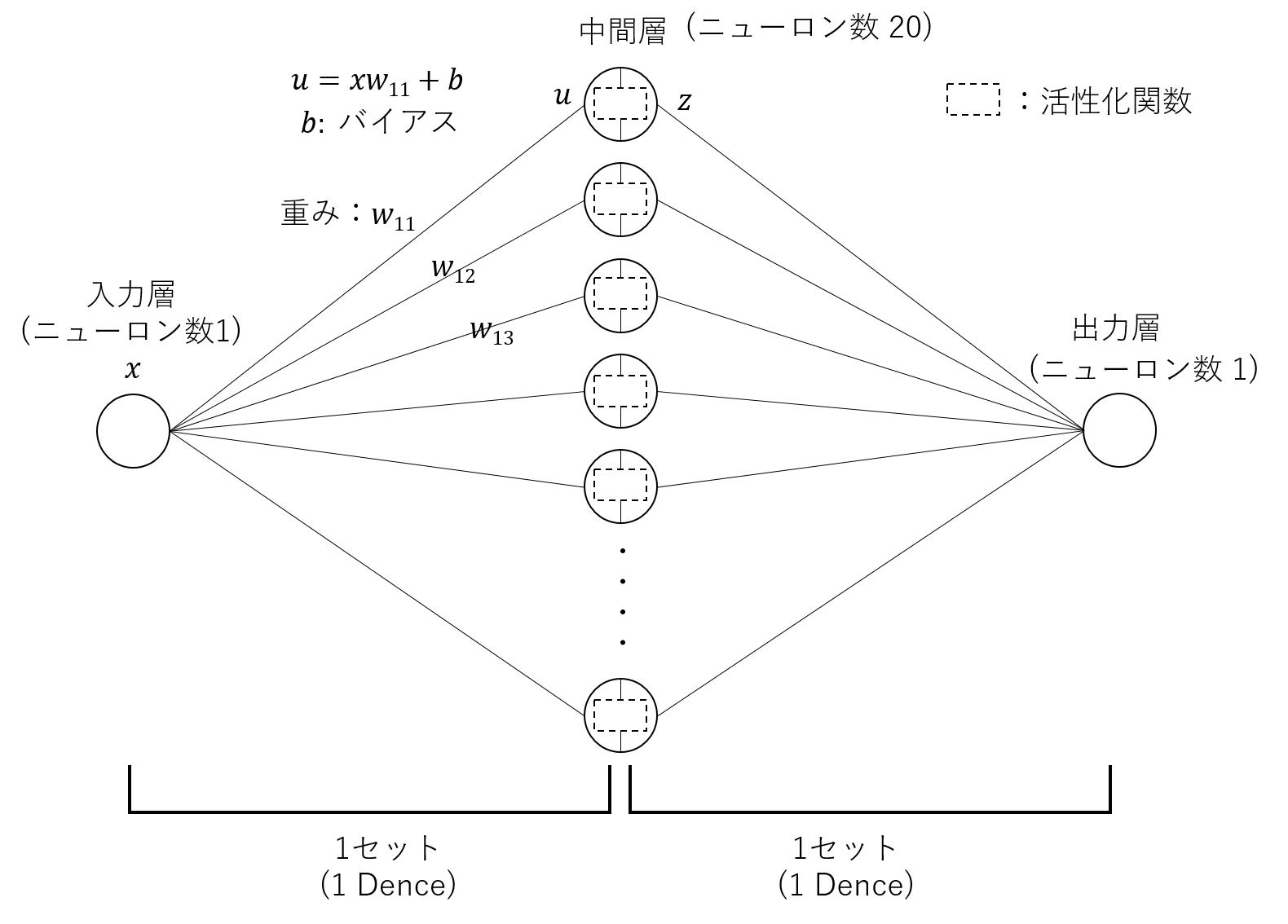
Dense({中間層のニューロン数}, {入力の形状}, {活性化関数})という記述になっています。

活性化関数というのは、中間層の各ノード(ニューロン)内で適用されるアルゴリズムで、下図における\( u \)から\( z \)を求める関数です。

活性化関数は、様々あり、自然言語処理の世界では、シグモイド関数、tanh(ハイパボリックタンジェント)、恒等関数が主となるようです。

今回は、シグモイド関数を使っていますが、他の活性化関数を適用して実験してみてもいいと思います。

また、こちらの\( u \)から\( z \)への変換を、非線形変換といったります。

線形でない曲線的な関数である、非線形の関数を用いて\( u \)から\( z \)を変換しているので、非線形変換といいます。

なぜ非線形なのでしょうか。線形変換でもよいのでは？と思うかもしれません。

理由は、ものすごく簡単に言ってしまうと、実際のビジネスでは、非線形なデータの方が多く、非線形変換を行わなければ、実際のビジネスの現場では使えないためです。

2セット目(中間層と出力層)の追加

続いて2セット目の層を追加します。

こちらもDenseを用います。

出力層のニューロン数と活性化関数を指定すればOKです。

コードとしては、model.add(Dense(n_out, activation="linear"))となります。

コンパイル

コンパイルというのは、人間が分かる言葉で書いたプログラムのコードを、コンピュータが分かる言葉に変換/翻訳することです。コンピュータが分かる言葉というのは、いわゆる0と1の列です。

コンパイルの際は、損失関数と、最適化アルゴリズム、というのを指定します。コードでいうと、model.compile(loss="mean_squared_error", optimizer="sgd")と記載しているところです。

損失関数とは、ニューラルネットワークが予想した値が静価値にどれだけ近いかを評価する関数のことです。

別名、評価関数とも呼びます。

損失関数は２つに分類されます。

• 回帰(数値を予測)　→　二乗誤差
• 分類(カテゴリを予測)　→　クロスエントロピー（交差エントロピー）

今回は、数値を予測するので、二乗誤差を指定しています。

最適化アルゴリズムとは、重み\( w \)をどのようなルールで変換して正解値に近づけるかを数式化(モデル化)したものです。

SGDとは、確率的勾配降下法というもので、数式としては、以下のようなものになります。

$$\overrightarrow{w}\leftarrow\overrightarrow{w}-\eta\dfrac{\partial E(\overrightarrow{w})}{\partial\overrightarrow{w}}$$

以下のページに詳しい説明がまとめられているので、興味のある方は参考にしてください。
https://mathwords.net/sgd

先ほどのコードを実行して、構築したモデルのsummary()を表示すると以下の通りとなります。

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 20)                40        
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 21        
=================================================================
Total params: 61
Trainable params: 61
Non-trainable params: 0
_________________________________________________________________
None

Output Shapeというのは、各Denseの出力側の形状を示しています。

1セット目(入力層から中間層の部分)のOutput Shapeは、(None, 20)となっているため、中間層のニューロン数が20であることを意味しています。

2セット目(中間層から出力層の部分)のOutput Shapeは、(None, 1)となっているため、出力層のニューロン数が1であることを示しています。

Paramというのは、各層のパラメータ数を示しています。

1セット目のパラメータ数が40(重みの数が20, バイアスの数が20の合計40)で、2セット目のパラメータ数が21(重みの数が20, バイアスの数が1の合計21)であることを示しています。

ニューラルネットワークを用いて学習

ここから、構築したニューラルネットワークを用いて学習を行います。

学習は、fit()メソッドを使います。

history = model.fit(x, t, batch_size=batch_size, epochs=2000, validation_split=0.1)  # 10%のデータを検証用に使う

modelのfitメソッドに、先ほどの入力xと正解t、バッチサイズ、エポック数、バリデーションスプリットを設定しています。

バリデーションスプリットとは、全データの何%を検証用のデータとして扱うかを指定することができます。今回は10%のデータを検証用に使うので、0.1を設定しています。

こちらのコードを実行すると以下のような出力が得られます。

Train on 45 samples, validate on 5 samples
Epoch 1/2000
45/45 [==============================] - 0s 5ms/step - loss: 0.5445 - val_loss: 0.0813
Epoch 2/2000
45/45 [==============================] - 0s 295us/step - loss: 0.3997 - val_loss: 0.0355
Epoch 3/2000
45/45 [==============================] - 0s 502us/step - loss: 0.3446 - val_loss: 0.0444
Epoch 4/2000

(略)


45/45 [==============================] - 0s 301us/step - loss: 0.0093 - val_loss: 0.1108
Epoch 1999/2000
45/45 [==============================] - 0s 265us/step - loss: 0.0093 - val_loss: 0.1142
Epoch 2000/2000
45/45 [==============================] - 0s 323us/step - loss: 0.0095 - val_loss: 0.1142

loss: となっている部分は、訓練用データの誤差になります。

10%の検証用データを用いた結果の誤差が、val_loss:として出力されています。

学習の推移をグラフで確認

matplotlibを用いて、先ほどのlossとval_lossをグラフとして描画してみます。

loss = history.history['loss']  # 訓練用データの誤差
vloss = history.history['val_loss']  # 検証用データの誤差

plt.plot(np.arange(len(loss)), loss)
plt.plot(np.arange(len(vloss)), vloss)
plt.show()

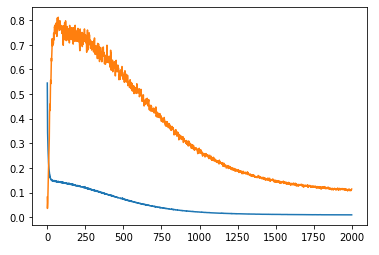
以下のようなグラフが表示されます。

検証用のデータは青いラインで、訓練用のデータがオレンジのラインです。

両者ともに、エポック数を重ねると順調に下がっています。

学習済ニューラルネットワークを使用して予測

predict()メソッドを用いることで、学習済みのニューラルネットワークを使用して予測を行うことができます。

plt.plot(x, model.predict(x))  # 予測を行う
plt.plot(x, t)
plt.show()

最初に、入力xと入力xをpredictメソッドに入れた結果をプロットします。

predictメソッドに入力値を渡すだけで、予測データの出力を得ることができます。

比較のために、入力xと正解値tをプロットしたものを同時に出力したいと思います。

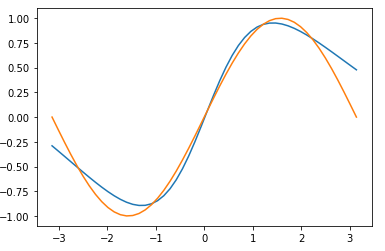
コードを実行すると以下のようなグラフが描画されます。

正解値はオレンジのラインで、学習済みのモデルに入力値を入れて予測したデータが青いラインになります。

正解のオレンジのラインをまねるように、青いラインが描かれていることから、ニューラルネットワークがサイン関数を学習していることが分かります。

Kerasでニューラルネットワーク(NN)を構築し学習/訓練、予測させる方法をまとめました。

本記事ではKerasでニューラルネットワーク(NN)を構築し学習/訓練、予測させる方法をまとめました。

ニューラルネットワークをちゃんと学びたい！という方はキカガクでの学習がおすすめです。

＼ 無料説明会受付中！ ／

キカガクを確認する

参考にしたページや文献など

• 確率的勾配降下法の大雑把な意味 - 具体例で学ぶ数学

• Optimizer : 深層学習における勾配法について - Qiita